Those of you who have been following NGS (National Geodetic Survey) plans for the rollout of a new NSRS (National Spatial Reference System) will already know that the incorporation of a temporal component makes the new system more than just “another adjustment.”
In the new NSRS, coordinates like latitude-longitude and Easting-Northing will now be time-dependent, and will require an additional piece of metadata — an “epoch” or date/time tag. Why do coordinates need an epoch? Because the Earth’s crust is moving. The location of every point — whether it’s a survey marker, a tree in your backyard, or the Washington Monument — is moving relative to the latitude-longitude graticule of the Earth. The movement may be small, but it’s definitely present.
Why does this movement occur? It’s all due to plate tectonics, the scientific theory that the Earth’s outer layer (the lithosphere) is composed of giant plates that move relative to each other, resulting not only in the aforementioned movement of features on the Earth’s surface but also mountain-building processes, earthquakes and volcanoes. The theory, first proposed in a different form by German scientist Alfred Wegener over 100 years ago, was initially scorned but is now widely accepted and has a great deal of empirical support. In Wisconsin we are located squarely on the North American Plate.
The Problem with Plate Tectonics
Drifting tectonic plates pose a problem for coordinate data. If we simply accept the fact that locations move, and make no adjustment for this fact, then using coordinates in ways we are familiar with becomes problematic. Every time we surveyed a location, its coordinates would change! How would we mix and match coordinates of different lineages to make a consistent map? Answer: We would not be able to.
The solution adopted by the NGS is to find a way to make locations appear to be stable, at least over finite time spans of years or decades. To do this, NGS created a series of reference frames — North America’s is called NATRF2022 — that are internally stable. Using equations that model the observed movement of the North American plate, we can then take a coordinate obtained at any specified epoch and compute its location at an earlier (or future) epoch. Using a collection of coordinates with the same epoch, we then have an internally consistent set of records to enable us to perform our mapping, surveying and GIS tasks.
Rotational Model
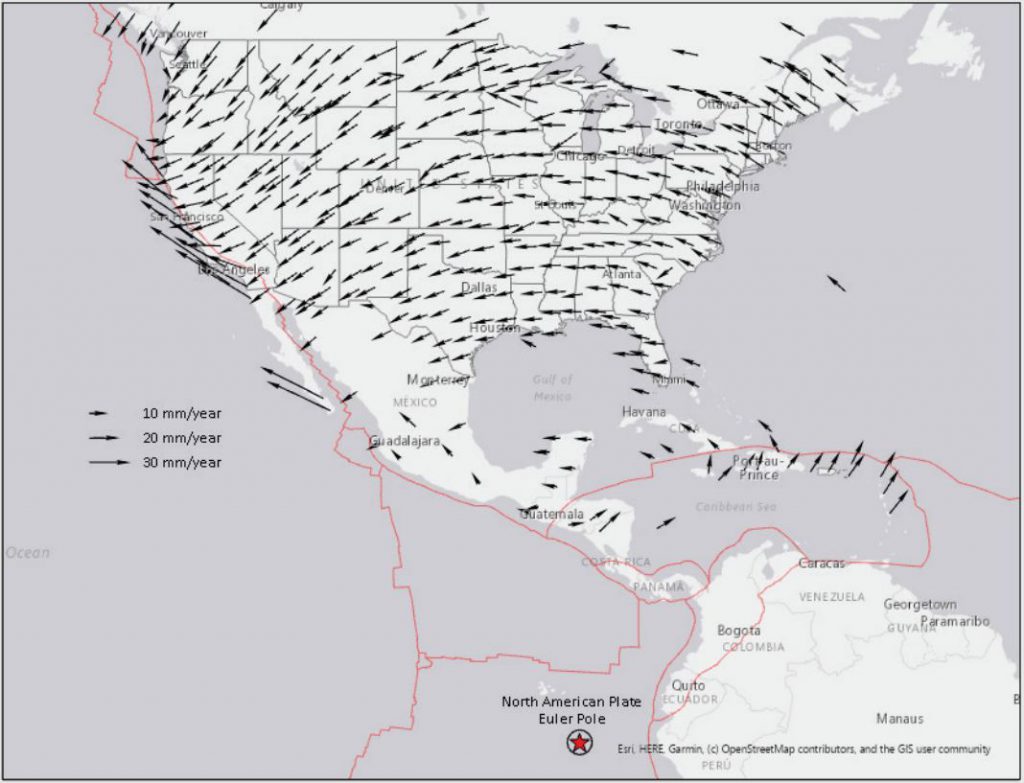
Continuously Operating Reference Stations.
(Source: NOAA Technical Report NOS NGS 62)
A “velocity vector” shows the direction and magnitude of movement for a given location. A map showing the observed velocity vectors for Wisconsin would present both systematic and seemingly random components. For Wisconsin, and most other other locations in North American, the systematic component is a counter-clockwise rotation around a fixed location known as the Euler Pole, which is located in the vicinity of the Galapagos Islands off the coast of South America. (See Fig. 1)
Finding the Euler Pole location and estimating the angular velocity with which the North American plate rotates around this pole has been determined using decades of precise measurements based on CORSs (Continuously Operating Reference Stations), GPS, GNSS and other technological magic. Once the pole location and the angular velocity have been determined, we end up with a fairly simple model that amounts to a 3-dimensional “affine” or “rigid motion” transformation. This is not rubber sheeting, since the plate is assumed to be rigid. It preserves the spatial relationships of all points on the plate relative to each other.
How much is Wisconsin rotating? That depends on where you are. According to the rotational model, the north part of the state moving faster, being farther away from the Euler Pole. In general, movement is under 2 cm per year, in a counter-clockwise direction. This means that if you have a 50-year old house, it has moved 1 meter since being constructed.
Non-Rotational Components
There’s one other piece of the model that’s also important here. If you observed the movement at any location over a long enough time period, you would note some slight variations from the rigid rotational movement. This is because tectonic plates are in fact not perfectly rigid, but exhibit local deformations including vertical movements that affect horizontal locations.
When the Euler-derived rotational component is eliminated from observed movements, the result is a set of seemingly random movements with velocities of several mm per year in Wisconsin. This is an order of magnitude less than the rotational component. The pattern for Wisconsin may appear random, but there is a systematic component to it. Over much of the state, locations are migrating slowly north toward Hudson Bay. This movement is ascribed to Glacial Isostatic Adjustment (GIA) related to the last ice. In effect the crust is rebounding upward due to the release of the pressure of ice upon it, even though this ice has been gone for tens of thousands of years. These vertical (elevation) changes cause associated shifts in horizontal location, since the vertical changes are non-uniform over space.
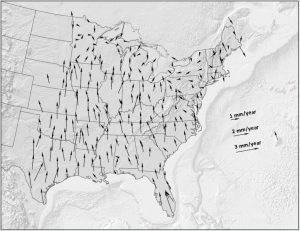
(Source: NOAA Technical Report NOS NGS 62)
In northern Wisconsin, non-rotational horizontal velocities are less systematic than in the south. Northern Wisconsin is believed to be part of a GIA “hinge line” with velocities trending in different directions on either side of the line.
NGS models these local, non-rotational velocities using an IFVM (Intra-Frame Velocity Model). The bottom line is that to accurately model movement of the plate and therefore accurately compute the location of a point at some epoch — other than the epoch at which the coordinate was actually observed — NGS must account for BOTH the rigid rotation around the Euler Pole as well as localized intra-plate velocities using the IFVM.
Want to Learn More?
More details on this topic can be found in the NGS’s updated Blueprint document, Blueprint for the Modernized NSRS, Part 1: Geometric Coordinates and Terrestrial Reference Frames.
If you have some spare time on your hands, you can also experiment with the NGS’s HTDP (Horizontal Time-Dependent Positioning) tool, which allows users to transform positional coordinates across time and between spatial reference frames.
